Конкурс "Системный администратор 2011" Опции

[Decker]

Официальная страница конкурса: http://admin2011.ru/ , http://sysadmin2011.ru/

Собственно заработал статус Гуру в тесте и набрал 380 баллов в квесте. Делиться здесь правильными ответами на этот раз не буду, т.к. действительно интересно сохранить дух соревнования, да и в интернете уже полно различных вариантов. А вот дать некоторые подсказки, наверное можно. Начнем с промо-кодов, которые добавляют +10 баллов в квесте каждый (ввод кодов доступен после прохождения квеста). Чтобы избавить вас от "мучительных поисков" в интернете, вот они:

1. rbrdcode
2. ideco4ever
3. imthebestadmin
4. adm11code
5. vk4adm11
6. summercode
7. adm11twi
8. bashcode
9. ideco4sysadm
10. freecode

Лента информации о конкурсе в Твиттере: http://twitter.com/#!/ideco_ru

Если кто-то "озадачился" поиском ответов на вопросы в тесте в интернете, могу сказать что ответ 42 на 14-й вопрос (тест на бинарное мышление) и "umount -f /dev/cdrom" на 13-й вопрос неправильные! В тесте на бинарное мышление необходимо проXORить зашифрованный текст с неким числом, после этого там получается вполне осмысленная фраза. На 13-й вопрос вы можете ответить самостоятельно.

Теперь что касается квеста. В вопросе где требуется составить программу для вывода какого-то слова на BrainFuck нам замечательно поможет ресурс http://www.deardeer.ru/ ... Например ссылка на этот форум на BrainFuck будет выглядеть следующим образом:

Код

++++++++++[>+>++>+++>++++>+++++>++++++>+++++++>++++++++>++++++++
+>++++++++++>+++++++++++>++++++++++++>+++++++++++++<<<<<<<<<<<<<
-]>>>>>>>>>>>------.>----..----.<<<<<<--.<---..>>>>>>----.++++++
+++.-.<<<<<<-.>>>>>-.>>-.<+.>+.<--.<--.>+.>+++++.<-----.<.<<<<<.
>>>>>>>---.+++.<<<<<<<+.

А QR-код с ссылкой:


QR код «QR - Quick Response - Быстрый Отклик» — это двухмерный штрихкод (бар-код), предоставляющий информацию для быстрого ее распознавания с помощью камеры на мобильном телефоне. При помощи QR-кода можно закодировать любую информацию, например: текст, номер телефона, ссылку на сайт или визитную карточку.

Программы для распознавания QR-кодов собраны тут. Лично я пользовался QuickMark'ом для Symbian.

Теги: конкурс системный администратор 2011, решение задач, алгоритмы, ответы, алгоритм поиска максимального пути (суммы) в треугольнике, получить статус гуру, промо-коды к конкурсу.

[Decker]

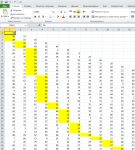
Про задачку в квесте с магическим треугольником ... 121x121 ... собственно я загрузил треугольник в Excel и написал на 1С 7.7 небольшую обработку, которая выбирала максимальное число для следующего шага (исходя из предположения, что если на каждом следующем шаге мы будем выбирать максимальное число, то и сумма, которую мы получим в результате прохождения всего пути будет максимальной), плюс раскрашивала пройденный путь в таблице XLS и подсчитывала сумму. Только вот это предположение неверно!

Я тоже так думал, пока не написал скрипт, который подтвердил мои догадки о возможности собрать большую сумму при переходах не на большее число в определенных местах. Представляю сколько математик будет одно только условие переписывать

Поясню задачу о треугольнике:

Пример. Дан треугольник:

2
1 3
4 1 5
4 1 7 1

С вершины (2), вы можете пойти либо на (1), либо на (3), если вы выбрали пусть на (3), следующим ходом вы можете пойти либо на (1) либо на (5), если вы выбрали (5), следующим будет выбор между (7) и (1). Для данного примера максимальная сумма будет 2+3+5+7=17

Так вот, если бы в нижнем левом углу стояло число 100500, то максимальная сумма как раз бы получилась в варианте в котором мы бы двигались только вниз.

Вот как это выглядело у меня:

К сожалению изначальный алгоритм, который лег в основу этой идеи был неверным.

[Decker]

Вообщем написал рекурсивный алгоритм ... положим что таблица значений Треугольник содержит искомый треугольник.


 tr.7z ( 12,1 килобайт ) Кол-во скачиваний: 61
- таблица в Excel'е с треугольником.

Тогда код для нахождения максимального пути можно представить как:

Функция СледующийШаг(i,j, Знач ПредСумма, МаксСтрок)
Перем Рез;
ПредСумма = ПредСумма + Треугольник.ПолучитьЗначение(i,j);
Если i=МаксСтрок Тогда
Рез = ПредСумма;
//Сообщить("Вариант: "+ Рез);
Возврат Рез;
Иначе
Рез = Макс(СледующийШаг(i+1,j,ПредСумма,МаксСтрок),СледующийШаг(i+1,j+1,ПредСумма,МаксСтрок));
Возврат Рез;
КонецЕсли;
КонецФункции

Процедура Запуск()
Зн = СледующийШаг(1,1,0,121);
Сообщить(Зн);
КонецПроцедуры

Правда вот на полный перебор уйдут столетия ... ибо количество вариантов для треугольника порядка n составляет 2^(n-1) вариантов ... т.е. посчитать рекурсивно - тоже не вариант )))

[Decker]

Итак, алгоритм переписан, т.к. 2^(n-1) комбинаций это чрезвычайно много и проводить полный перебор смерти подобно. Например для треугольника 20x20 (элементы треугольника взяты из таблицы):

Код

Сумма пути: 1406
Количество вариантов: 524288
Время формирования: 19.822 сек.

Будем двигаться от противного. Предполагаем что мы можем закончить подсчет максимальной суммы пути абсолютно на любом числе из последней строки. Возникает вопрос. Как же мы можем на него попасть? Варианта всего два, либо это элемент над ним, т.е. верхней элемент, либо элемент по диагонали слева-сверху. Введем несколько условий ограничивающих число вариантов. Во-первых, на элемент находящийся в первой колонке мы можем попасть только с верхнего элемента, во-вторых, на элемент находящийся на диагонали мы можем попасть только с левого-верхнего элемента, ну это и так понятно. Дальше интереснее. Предполагаем изначально что мы могли перейти к текущему элементу, либо с левого-верхнего, либо с верхнего. Если элемент справа больше нас, то с верхнего элемента мы попасть сюда не могли, т.к. на каждом шаге мы должны выбирать максимальный элемент, т.е. мы попали сюда с левого-верхнего элемента. Однако, если при этом элемент слева больше нас, то получается что слева-сверху мы сюда тоже попасть не могли, и этот вариант совсем выбрасывается из рассмотрения. В оставшихся случаях получается что мы могли попасть сюда как слева-сверху, так и сверху, следовательно проверяем оба варианта. Все эти предположения помогут нам сократить количество вариантов. Т.о. выбираем последовательно элементы последней строки и предполагаем что мы достигли максимальной суммы именно на этом элементе (т.е. именно он был последним шагом), затем руководствуясь описанным выше алгоритмом выбираем предыдущий элемент и так далее рекурсивно до начала треугольника. В результате получаем n (где nxn - размер треугольника) сумм, среди которых выбираем максимальную, она и будет искомой. Так например, для того же треугольника 20x20 получим:

Код

Сумма пути: 1406
Количество вариантов: 125
Начали с: 89
Время формирования: 0.098 сек.

Разница во времени существенна, как вы видите.
А для треугольника из 22 элементов получается соответственно:

Код

Сумма пути: 1520
Количество вариантов: 2097152
Время формирования: 89.526 сек.

и

Код

Сумма пути: 1520
Количество вариантов: 227
Начали с: 53
Время формирования: 0.145 сек.

если использовать обратный алгоритм.

p.s. К сожалению этот алгоритм также был неверным ... поэтому я его отсюда убрал.

[Decker]

Хм ... вообщем-то что хотелось сказать ... путь можно выбирать любой (!), т.е. не факт что максимальная сумма будет там где мы на следующем шаге выберем максимальное число. Еще раз прочитаем цитату:

Я тоже так думал, пока не написал скрипт, который подтвердил мои догадки о возможности собрать большую сумму при переходах не на большее число в определенных местах. Представляю сколько математик будет одно только условие переписывать

Ну и вот еще размышления на тему:
http://projecteuler.net/index.php?section=problems&id=18
http://euler.jakumo.org/problems/view/67.html - Задача 67. Нахождение максимальной суммы треугольника с помощью эффективного алгоритма.
http://flmyshe.tk/uncategorized/maximum-sum-of-triangle/ - решение на Java (и описание алгоритма)
http://www.peterkrantz.com/2009/project-euler-in-ioke/ - Problem 18
http://blog.singhanuvrat.com/problems/proj...m-in-a-triangle
http://www.tushar-mehta.com/misc_tutorials...r/euler018.html - вот здесь наглядно описывается решение

Алгоритм:

1. Start from the top of the triangle, move down one level at a time.
2. For each level, start from left to right, find the max sum of the adjacent fields in the previous/upper level, add the max sum to the current value and store the new max sum in the current field. Move to the next field and repeat this step until the end of the current level.
3. Repeat the above step until you reach the end of the last level in the triangle
4. Find the maximum number in the lowest(bottom) level. This is the maximum total of the triangle.

[Decker]

Solution

These kind of problems are best solved by working "backwards." Look at row 14. Suppose that somehow we include the 63 in our summation. Then, which value will be pick in row 15? Since our choices are 04 or 62, we will pick the 62. Similarly, suppose we had reason to include the 66 in our sum. Then, which value will be pick in row 15? Given our choices of 62 or 98, we will pick 98. So, we can replace the 63 in row 14 with 125 and the 66 in row 14 with 164. We do the same with all the elements in row 14. Now, we no longer need row 15 in our calculation. Next, we look at the numbers in row 13. Suppose we were to somehow pick the 91. Then, given the new values in row 14 of 125 and 164, we would pick the 164 meaning the 91 in row 13 can be replaced by 255. Continue this analysis all the way to row 1 and we will get the desired result. We can implement this in Excel as follows.

Enter the triangle in a way that looks like a right-triangle but it will still be the same kind of tree as above. For any given number, the two choices are in the row just below that number. The first is just under the number and the other number is the one just to the right.

http://www.tushar-mehta.com/misc_tutorials...er018-img5D.png

Now, copy the last row into some other row that has 15 empty rows above it. I chose row 35. Then, in A34 enter the formula =MAX(A35:B35)+A14 Copy this up column A to A21:A33 and then copy A21:A34 to B:O. One could clean up the cells so that there is only one leftmost cell in row 21, 2 leftmost cells in row 22, and so on down to 14 cells in row 34. Or, one could leave the formulas alone and simply look at the contents of A21 since that is the answer!

Эскизы прикрепленных изображений

 

[Decker]

Эффективный алгоритм поиска максимального пути (максимальной суммы) в треугольнике.

Реализация на 1С (с) Decker

Рассмотрим на треугольнике 5-го уровня:

Код

74
78 22
28 10 16
17 35 10 61
78 86 48 18 49

Посмотрим на предпоследнюю строку с номером 4. Предположим что число (17) входит в наш путь, т.е. в нашу сумму. Какое следующее число мы выберем чтобы сумма была максимальной? Я думаю что мы выберем 86, итого на последнем шаге получаем 17+86=103. Двигаемся по предпоследней строке далее, сейчас мы стоим на числе (35). Что мы выберем на следующем шаге? 86 или 48? Естественно 86, т.к. 35+86 = 121. Далее, число (10). С него можно пойти либо на (48), либо на (18). Конецчно же мы выберем (48), т.к. 10+48=58. Ну и так далее до конца строки. А теперь мы просто заменим все числа в строке 4 на полученные суммы. Т.е. 17 заменим на (103), 35 заменим на (121), 10 заменим (58) и так далее. Повторим данную операцию со строкой (3) ... и далее, вплоть до строки (1). В результате в первой строке мы получим искомую максимальную сумму.

Итого получаем два алгоритма, прямой-рекурсивный, в котором рассматриваются все варианты (напомню что для треугольника 15 порядка существует 16384 путей, т.е. 2^14 ... для треугольника порядка n число путей равно 2^n-1, т.е. для порядка 121 мы будем считать бесконечное количество лет, и наши внуки наших правнуков с многочисленными приставками пра-, участвующие в конкурсе Сисадмин 4011 наконец-то получат решение Поэтому этот метод, перебирающий все пути подходит только для треугольников небольшого порядка. Еще раз приведем функцию на 1С 7.7 для расчета суммы по этому методу:

Функция СледующийШаг(i,j, Знач ПредСумма, МаксСтрок)
Перем Рез;
ПредСумма = ПредСумма + Треугольник.ПолучитьЗначение(i,j);
Если i=МаксСтрок Тогда
Рез = ПредСумма;
//Сообщить("Вариант: "+ Рез);
Возврат Рез;
Иначе
Рез = Макс(СледующийШаг(i+1,j,ПредСумма,МаксСтрок),СледующийШаг(i+1,j+1,ПредСумма,МаксСтрок));
Возврат Рез;
КонецЕсли;
КонецФункции

Процедура Запуск()
Зн = СледующийШаг(1,1,0,121);
Сообщить(Зн);
КонецПроцедуры

А вот кусок эффективного алгоритма для расчета максимальной суммы пути в треугольнике:

//*******************************************
Процедура ЭффективныйАлгоритм()

Таймер = _GetPerformanceCounter();
ОчиститьОкноСообщений();

ВремТЗ = СоздатьОбъект("ТаблицаЗначений");
Треугольник.Выгрузить(ВремТЗ);
i=ПорядокТреугольника-1;
Пока i > 0 Цикл
Для j=1 По ПорядокТреугольника-1 Цикл
Зн = ВремТЗ.ПолучитьЗначение(i,j)+Макс(ВремТЗ.ПолучитьЗначение(i+1,j),ВремТЗ.ПолучитьЗначение(i+1,j+1));
ВремТЗ.УстановитьЗначение(i,j,Зн);
КонецЦикла;
i = i - 1;
КонецЦикла;
Сообщить("Сумма пути: "+ВремТЗ.ПолучитьЗначение(1,1));

ТаймерВыводаОтчета = (_GetPerformanceCounter() - Таймер)/1000;
РезультатВыводаОтчета = "Время формирования: "+ТаймерВыводаОтчета+" сек.";
Сообщить(РезультатВыводаОтчета);

КонецПроцедуры

Работает этот алгоритм крайне быстро на треугольниках любого порядка. Ну а сумму пути, я вам не скажу Если вы все поняли, то без труда перепишите этот алгоритм на любой язык, или выполните все описанные действия в Excel'е.

p.s. Просто полезная тема про конкурс - http://m.freehabr.ru/blog/741.html
p.p.s. Кстати метод эффективного алгоритма вроде бы называется «Золотая гора»

[Decker]

Так что самое время выпускать конфигурацию 1С:Решение треугольников

Еще одно мое мнение:

Кстати, кто там в тест и квест играл на http://sysadmin2011.ru/ ? В тесте набрал Гуру ... нагугленные ответы кстати не совсем правильные, например, в вопросе про бинарную зарядку для ума (где нужно проXORить зашифрованный текст со звездочкой) ... ответ далеко не 42, а слово. А вот в квесте ... в квесте последний вопрос убил наповал ... это тот который "При развертывании локальной сети масштаба предприятия, состоящей из 1000 компьютеров и 18 маршрутизаторов, было принято решение использовать ячеистую топологию (cell-topology). Во сколько раз можно существенно сократить внутрисетевого трафика за счет перехода на кольцевую топологию или FDDI" ... если кто посчитал и уверен что ответ верный, интересна методика подсчета и принципы, которыми вы руководствовались. Как по мне, этот вопрос бредовый ... равно как и КОШКА + КОШКА + КОШКА = СОБАКА ... А вот с треугольником, там где нужно максимальную сумму пути найти - интересно вышло ... Написал на 1С 7.7 обработку для подсчета (собственно это первое что было открыто в момент когда я проходил это задание ))) ... На самом деле все крайне просто считается по алгоритму "золотой горы" ... можно и рекурсивно, но только для треугольников малых порядков ... 121x121 так не сосчитать. Вообщем кому интересно пообщаться по поводу конкурса, вот здесь есть некоторые мои мысли )