Алгоритмы / [Из песочницы] Японские кроссворды и алгоритмы их решения Опции

[Decker]

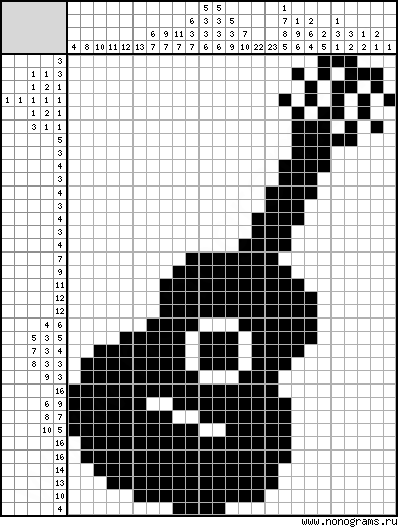Недавно мне выпала следующая задача: написать программу, находящую все решения или их отсутствие для данного японского кроссворда размера NxM. Далее представлены 4 алгоритма решения японских кроссвордов.



Для тех кто не знает что такое японский кроссворд- ссылка на википедию.



Японский кроссворд представляется в памяти в виде двух матриц. Первая размера NxM хранит поле. Закрашенная клетка обозначается 1(один), незакрашенная 0(ноль), неизвестная -1(минус один).

Вторая хранит N кодов строк и M кодов столбцов, заканчивающихся нулем.



Первый алгоритм.

Первым, что я написал, был алгоритм перебора. Поле NxM заполняется 1 и 0. И для каждой строки и каждого столбца проверяется соответствие коду.

Несложно посчитать количество вариантов такого заполнения. Их ровно 2^(N*M). Сложность алгоритма O(2^(N*M)).

Работает достаточно быстро лишь на маленьких кроссвордах (размера не более 15x15).



Второй алгоритм.

Второй алгоритм представляет из себя более умный, но все же, перебор. Теперь поле заполняется не отдельными единицами, а целыми блоками. Берутся строки и заполняются блоками, длины и порядок которых берутся из соответствующих кодов. Затем для каждого столбца проверяется соответствие своему коду.

Очевидно, самый худший вариант- когда все коды строк равны «1, 0» (тоесть 1 блок из 1 клетки). Количество вариантов размещения таких блоков равно M^N. Сложность алгоритма O(M^N).



Следующие алгоритмы уже не являются алгоритмами перебора, но существуют кроссворды которые невозможно решить не используя перебор и кроссворды с огромным количеством решений (например кроссворд NxN, каждая строка и каждый столбец которого состоит из 1 блока единичной длины, имеет N! решений). В конце концов для каждого из таких кроссвордов приходится запускать перебор.



Третий алгоритм.

Третий алгоритм я нашел на следующем сайте. Исходники на паскале так же можно найти на этом же сайте.

Суть алгоритма:

Для каждой строки и каждого столбца строятся всевозможные непротиворечивые (по отношению к уже известным клеткам) расположения блоков и клетки, которые при всех расположениях остаются закрашенными(незакрашенными), отмечаются на поле соответствующей цифрой. Если ни одного расположения не существует- значит кроссворд имеет противоречие.



Четвертый алгоритм.

Четвертый алгоритм основан на использовании конечных автоматов. Если есть желание, можно прочитать что это такое на википедии. Но большого смысла я в этом не вижу, так как принцип работы конечного автомата и так будет понятен.



Можно считать, без ограничения общности, что мы работаем со строкой и ее кодом.



s — строка.

size2 — длина строки.

size1 — длина схемы автомата.



1) Первый шаг алгоритма- построение схемы автомата.

Пример схемы автомата для кода «4,1»:



(-1,1,1,1,1,0,-1,1,-1),

Где

-1 это произвольное количество незакрашенных клеток (Может быть и 0 незакрашенных клеток),

1 это одна закрашенная клетка,

0 это одна незакрашенная клетка.



2) Второй шаг- попытка принять строку автоматом.

— Создание массива размера size1x(size2+1).

— Заполнение первого столбца массива схемой конечного автомата.

— Остальные элементы массива заполняются -1.

— Заполнение массива.



Функция, заполняющая массив.1.cpp



Пример заполнения массива для строки (-1,-1,-1,1,-1,-1,-1,-1,0,-1) и схемы автомата для кода «4,1» (-1,1,1,1,1,0,-1,1,-1).







Массив заполняется диагональными путями. Каждый путь соответствует одному из расположений блоков «4» и «2» в строке. Например путь, выделенный на картинке, соответствует строке (0,1,1,1,1,0,0,0,0,1)/



3) Третий шаг- извлечение информации из полученного на 2 шаге массива.

— Если в i столбце кроме -1 содержаться 1,0 то клетка s[i-1] может быть и закрашенной и незакрашенной.

— Если в i столбце кроме -1 содержаться только 1 то клетка s[i-1] может быть только закрашенной.

— Если в i столбце кроме -1 содержаться только 0 то клетка s[i-1] может быть только незакрашенной.



В предыдущем примере заполнения массива информация извлекается только из 5 и 10 столбца. Клетка s[4]=1 и s[9]=0, что и так было известно.



Рабочая версия программы: Japan.rar

Original source: habrahabr.ru (comments, light).

Читать дальше